Preferred numbers and sizes in engineering and design
There is a preferred numbers and sizes system in engineering design, worldwide. Here’s the explanation.
What do balloons have to do with engineering sizes ?

In the 1870s, the French military was trying to use navigable balloons – called airships, or dirigibles – for transport (the airplane was only invented in 1903). A large number of ropes were required to tie a balloon to the ground and prevent it from flying away. Charles Renard, a military engineer, reduced the different diameters of rope used from 425 to 17.
He invented the ‘Preferred number system’, which specified that you could use only certain sizes. The preferred numbers are a geometric series, each number a multiple of the one before it. The factor between two consecutive numbers can be the 5th, 10th, 20th, or 40th root of 10 (approx. 1.58, 1.26, 1.12, and 1.06, respectively). These are called R5, R10, R20 and R40.
R5 leads to a coarse 60 % increment, R10 to a finer 25 % increment, R20 to even finer 12 % increment. To get each successive size, you multiply the previous number by the factor and then round it off.

The preferred numbers and sizes are used in virtually anything you can think of on the shop floor. E.g.,Fastener sizes, plate thicknesses, thread sizes, tool diameters, tolerances.
Example of thread sizes
R5 (factor 1.58) : M2.5, M4, M6, M10, M16, M24
R10 (factor 1.26): M3, M5, M8, M12, M20, M30
Example of face milling cutter diameters (R10, factor 1.26)
40, 50, 63, 80, 100, 125, 160, 200
Renard numbers have now become the ISO 3 standard.

Transform production and profits dramatically, in just a few months.
With a CNC machine monitoring system.
Etc
Preferred numbers in nature – Fibonacci numbers
Surprisingly, nature has a preferred number system too – the Fibonacci sequence (pronounced Feebonachchi).
In this sequence, each number is the sum of the two numbers before it.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
(0+1=1, 1+1=2, 1+2=3,2+3=5, etc.)
Bananas have 3 or 5 sides, flowers have 3/5/8 etc. petals, tree branches grow in a Fibonacci sequence, human finger lengths follow the sequence. Virtually everything in nature follows this.

Spirals in nature are Fibonacci spirals – the distance from the centre keeps increasing in a Fibonacci sequence.
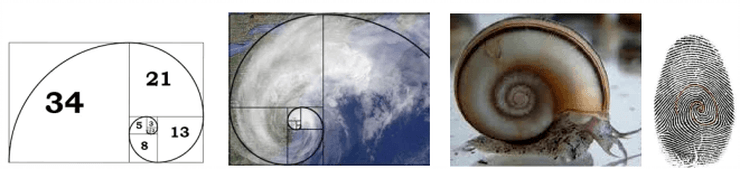
Amazing that there’s so much maths in nature !
Sorry about getting so mathematical in this post, in both the CNC and Etc parts. Hope it doesn’t spoil the fun of appreciating nature from now on, like your brain automatically cross-checking with the Fibonacci sequence every time you look at a flower’s petals.
It definitely spoilt my fun of eating one of my favourite fruits, the banana. Now each time I’m eating a banana I have to see how many sides it has ![]() .
.